Image Kernels
Subject Matter
In Week 1, professor Malan has gone over the way computers represent images. In the “Background” section of the problem, we also got a deeper look into the bits and bytes of such representation. However I think it’s still worth it to take a step back and unravel, step by step, how digital images work, how knowledge of their inner mechanism drives our mathematical models, and how such insights can help us write clearer, more readable algorithm.
Pixels
Today’s world is packed with digital displays: TVs, smartphones, laptops, etc…, and we are constantly interacting with them. But have you ever wondered how does those little rocks show videos, applications, images? Let’s try zooming into them, and see what’s up under the hood.
There’s a lot to observe here, let’s try to list them.
- We can see a recurring pattern of tiny blue, green, and red LEDs.
- These LEDs can be lit up, either completely or dimly, or they can be put out,.
- They are organised in a very intentional manner, resembling a square grid, or a chess board.
- Each pattern has four identical neighbors, shares its edges with them, and together they fill the plane with negligible gaps.
- All edges are either horizontal or vertical, and the patterns all align in both directions
From these observations, it’s seems like a good idea not to think of each LEDs as separate individuals, but as components of a group. It’s also feel natural to give the group a name. So let’s call them pixels, short for picture elements, as they seemingly are the smallest constructing components of a digital image.
Using these newfound knowledge, let’s try to design a model to represent these picture elements.
Coordinate Systems
Let’s start with thinking about the way to reference these pixels. Referring them with unique names like “John” or “Mary” won’t work: as there’s also no individuality nor meaning in one isolated three-coloured light group, giving them character would bring avoidable complication.
So rather than using these normal addressing methods, let’s use coordinate systems - mathematical frameworks that’s universally objective. They come in all shapes and sizes, ranging from simple and straightforward to obscure and hyper-specific. If you can think of it, there’s probably a coordinate system for it. So as to not reinvent the wheel, let’s try and find a suitable coordinate system to achieve our goal.
Repurposing Cartesian Coordinates
Luckily for us, we don’t need to look far and wide for a promising candidate to show up, as they are practically with us right from the start - Cartesian Coordinates. Just to be sure, let’s take another look at our familiar friend.
Now let’s see why this system seems so compelling for our problem:
- Both Cartesian coordinates and our pixels grid are aligned in horizontal and vertical straight lines.
- As most images and devices that display them are rectangular, they naturally fits in the system’s grid.
- They are simple, intuitive, and ubiquitous. Most students encounter it as early as elementary school.
A solid start, but I have already spotted an issue. We want our values to be positive whenever possible, which means currently only the first quadrant is a viable choice. However, doing so means the first pixel will be at the bottom, and the last pixel at the top. This contradicts how we read, images or text, which is generally top-to-bottom.
A simple fix is simply flipping the Y-axis around.
Pixels Coordinates
With our system done, let’s try putting some pixels on it. I will also introduce some new panels to keep track of them as well.
This feels a bit arkward, don’t you think? Let’s add a button to clean our canvas, and go again. This time thinking about what is going wrong.
Indeed, we are trying to represent pixels, a 2D object, with points, a 1D entity. Sure, we can draw a set of points to represent 2D shapes, but multiple coordinates would be needed to accommodate a single object, creating avoidable complication.
Another issue is the appearance of floating-point numbers. We don’t think of pixels in parts: just like a human can’t be divided in half, the concept of a half-pixel holds no meaning. Thus, while those numbers enabled us to take accurate measurements, such precision isn’t needed right now.
How can we resolve this? The solution is deceptively simple: shifting the axes’ labels.
What has we achieved here? Before, each number correspond to a line. Now, the same numbers, just positioned a little leftward (or upward, in the Y-axis), represent columns. The intersection of two lines creates a point, while the intersection of two columns creates a cell, closely mimicking the characteristics of the pixels. The labels shift also eliminate floating-point numbers from our system, as there’re no longer any “gaps” for them to fit in.
Let’s see if it works in practice.
Much better! Now let’s reintroduce our “Clear Pixels” button to see if we can spot anything odd.
Currently, multiple pixels can occupy the same area. Strictly speaking, in one memory address, there’s only one pixel. So letting a coordinate hold more than one isn’t exactly correct here.
That said, in real life, as you put more paint over and over again in the same spot, the pigments will accumulate, increasing their “density”, until the paper simply can’t hold any more of them. The effect is that the color will gradually increase in saturation and value, which is exactly what happened here. Since we have a good reason to keep this “bug”, I’ll just let it be (totally not because I don’t want to optimize my code).
A more important issue is in the way we are handling our labels. At first glance, a coordinate like (1, 1) is intuitive for us humans to understand that it is referring to the pixel in the intersection of the first horizontal and vertical column. But as you should know by now, the first element of anything for computer scientists is actually represented by the number 0. So let’s shift our labels again, this time to the right (X-axis) and downwards (Y-axis).
By this point, I think our modified system have strayed far enough from the source that it deserves it own name. Pixel coordinates seems fitting. After all, it is tailor-made to represent pixels.
Image Kernels & Image Convolution
The Filters problem culminate in having you implementing a Sobel operator. In which you are supposed to slide a 3x3 rectangular array of numbers, called kernel, over an image. At each position, the values of our kernel are multiplied by the corresponding values of the pixels that they “cover”, then added together to produce a single value. This value is then assigned to a coordinate in the output image, which is decided by the kernel’s origin or anchor point.
A single instance of such series of action is called a convolution. The result of a convolution refers to both the computed value and the output location of the value.
Let’s try to represent a convolution in our new coordinate system, starting from the kernel.
Just like how a 2D shape can’t be defined by one single point. A kernel can’t be defined by only one single cell. To define any actual shapes, we need additional information, whether it is in the form of the shapes’ vertices, dimensions, orientations, etc.
By convention, a kernel is described by the coordinates of its center cell plus its dimensions, however, any other methods will work as fine.
Next, let’s place an input image. As I’m too lazy to let you upload your own, we will use an image of a cube. I will also create an area to indicate their potential placement.
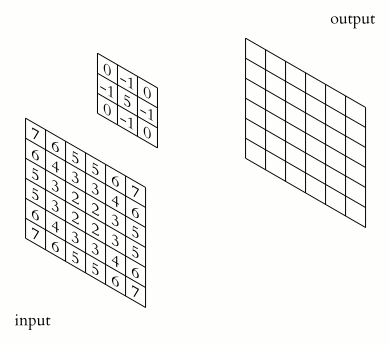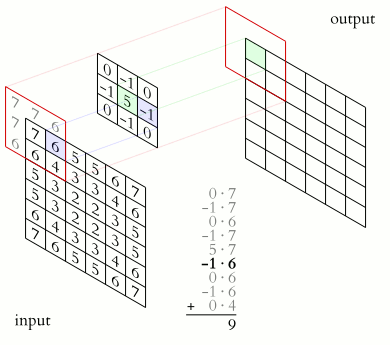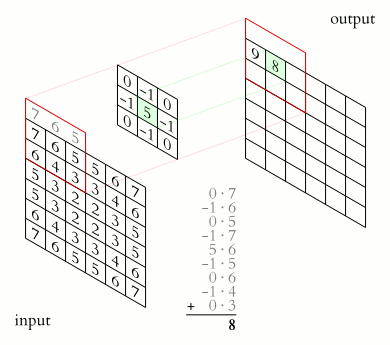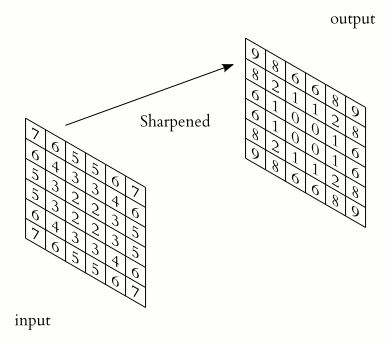
Now, let’s give each cell in the kernel a value and create a new panel so we can see the computations at each position. Sometimes we can also refer the part of an image that a convolution currently process its “window” (this makes a lot of sense when you think about it: if what we are “seeing through” is the kernel, then what we actually see are the pixels behind it).
Finally, let’s put those computed values into our output images. Click on any points in the input grid to choose the origin. Then drag the kernel around to see the convolution result.
Let’s add some buttons to reset the convolution process, and run it over again to see if we can notice anything interesting.
There’s a lot to unpack here, I will list what I observed, in no particular order:
- In one image, a single convolution window in a unique coordinate processed by one kernel will produce a single value.
- A single convolution value can be placed anywhere in the output image.
- The placement of such value is decided by the chosen origin.
- In one complete convolution of the image, if the relative position between the kernel and its origin is unchanged, one unique convolution window can be perfectly mapped to one unique location in the output image, and vice versa.
Point #4 is of particular interest for us. Why? It implies that if the output coordinates and kernel values are fixed, then the sole factor deciding the resulting image is the relative position of the kernel to its origin.
To see the effect, let’s reverse the model around. Place the kernel, then use your keyboard (space/D key/Right Arrow) to scan over the image.
And as for every image filters, we only change the values of each pixels without touching their positions. Meaning the calculation to find the coordinate of the window that hold the convolution value of given pixel can be as simple as a vector addition. From this, the complete convolution of an image can be described as:
- Calculate the relative position.
- For each coordinates in the input image, find its corresponding convolution window.
- Calculate the value of that window.
- Put the calculated value to the target pixel in the output image based on the coordinates of the input.
Note that this whole operation is only possible because of the premise that the output and input has the same dimensions and placements within the pixel coordinates. If they are different, like in scaling or rotating operations for example, it would be an entirely different ball game.
Roundup
Today, I have (hopefully) shown you how the need to find a better solution to a problem drives innovation. As well as how we derived an algorithm to describe an abstract object based on observation and reasoning.
As a side note, the pixel coordinate that we described today is can bed used for anything that’s “discrete”, whether they are people in lines or books on the bookshelf. This study of such objects is the principle concern for the field of discrete mathematics.
Congratulations for making this far. As a reward, here is a game that didn’t make the cut.
-
By Michael Plotke - Own work, CC BY-SA 3.0 ↩